This post is by Lisa Mannel, Scientific Assistant in the Process And Data Science group at RWTH Aachen University. Contact her via email for further inquiries.
Our paper „Finding Complex Process-Structures by Exploiting the Token-game“ has been accepted for publication by the 40th International Conference on Applications and Theory of Petri Nets and Concurrency.
In our paper we present a
novel approach to process discovery. In process discovery, the goal is to
find, for a given event log, the model describing the underlying process. While
process models can be represented in a variety of ways, in our paper we focus
on the representation by Petri nets. Using an approach inspired by
language-based regions, we start with a Petri net without any places, and then
insert the maximal set of places considered fitting with respect to the
behavior described by the log. Traversing and evaluating the whole set of all
possible places is not feasible, since their number is exponential in the
number of activities. Therefore, we propose a strategy to drastically prune
this search space to a small number of candidates, while still ensuring that
all fitting places are found. This allows us to derive complex model structures
that other discovery algorithms fail to discover. In contrast to traditional
region-based approaches this new technique can handle infrequent behavior and
therefore also noisy real-life event data. The drastic decrease of computation
time achieved by our pruning strategy, as well as our noise handling
capability, is demonstrated and evaluated by performing various experiments.
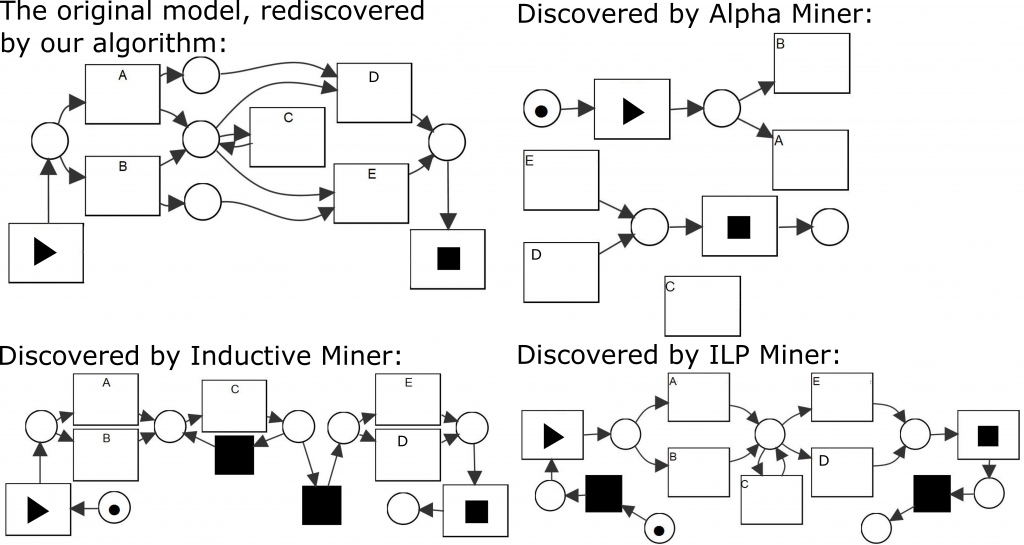
Figure 1: Consider the model shown in the upper left and assume L to be a complete log describing the behavior of this model. There exists a variety of discovery algorithms that are able to mine a process model based on L. As illustrated, the resulting Petri nets differ significantly between the algorithms. In particular, the places connecting A to D and B to E, which ensure that the first choice implies the second choice, are rarely discovered by existing algorithms.
You can download the full text here.

