New Gartner Magic Quadrant for Process Mining Platforms Is Out
In 2023, Gartner published the first Magic Quadrant for Process Mining. This reflected that analyst firms started considering process mining as an important product category.
On April 29th 2024, the new Gartner Magic Quadrant for Process Mining Platforms was published. The Magic Quadrant (MQ) is a graphical tool used to evaluate technology providers, facilitating smart investment decisions through a uniform set of criteria. It categorizes providers into four types: Leaders, Visionaries, Niche Players, and Challengers. Leaders are well-executed and positioned for future success, whereas Visionaries have a clear vision of market trends but lack strong execution. Niche Players focus on specific segments without broader innovation, and Challengers perform well currently without a clear grasp of market direction.

Prof. Wil van der Aalst (c) PADS
In the 2024 MQ, five new vendors were added, and two were dropped, leading to 18 vendors being compared. Twelve additional vendors received an honorable mention. Overall, there are currently around 50 process mining vendors (see www.processmining.org). According to Gartner, “By 2026, 25% of global enterprises will have embraced process mining platforms as a first step to creating a digital twin for business operations, paving the way to autonomous business operations. Through 2026, insufficient business process management maturity will prevent 90% of organizations from reaching desired business outcomes from their end-to-end process mining initiatives.” This illustrates the relevance of the Process Mining MQ.
For the second year in a row, Celonis has been the highest ranked in terms of completeness of vision and ability to execute. Other vendors listed as leaders are Software AG, SAP Signavio, UiPath, Microsoft, Apromore, Mehrwerk, Appian, and Abbyy. The basic capabilities provided by all tools include process discovery and analysis, process comparison, analysis and validation, and discovering and validating automation opportunities. New and important capabilities include Object-Centric Process Mining (OCPM), Process-Aware Machine Learning (PAML), and Generative AI (GenAI).
For more information, download the report from https://celon.is/Gartner.
Conformance Checking Approximation Using Simulation
This post is by Mohammadreza Fani Sani, Scientific Assistant in the Process and Data Science team at RWTH Aachen. Contact her via email for further inquiries
Conformance checking techniques are used to detect deviations and to measure how accurate a process model is. Alignments were developed with the concrete goal to describe and quantify deviations in a non-ambiguous manner. Computing alignments has rapidly turned into the de facto standard conformance checking technique.
However, alignment computations may be time-consuming for real large event data. In some scenarios, the diagnostic information that is produced by alignments is not required and we simply need an objective measure of model quality to compare process models, i.e., the alignment value. Moreover, in many applications, it is required to compute alignment values several times.
As normal alignment methods take a considerable time for large real event data, analyzing many candidate process models is impractical. Therefore, by decreasing the alignment computation time, it is possible to consider more candidate process models in a limited time. Thus, by having an approximated conformance value, we can find a suitable process model faster.
By providing bounds, we guarantee that the accurate alignment value does not exceed a range of values, and, consequently we determine if it is required to do further analysis or not, which saves a considerable amount of time. Thus, in many applications, it is valuable to have a quick approximated conformance value and it is excellent worth to let users adjust the level of approximation.
In this research, we extend the previous work by proposing to use process model simulation (i.e., some of its possible executable behaviors) to create a subset of process model behaviors. The core idea of this paper is to have simulated behaviors close to the recorded behaviors in the event log. Moreover, we provide bounds for the actual conformance value.
Fig 1. A schematic view of the proposed method.
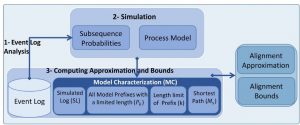
Using the proposed method, users can adjust the amount of process model behaviors considered in the approximation, which affects the computation time and the accuracy of alignment values and their bounds. As the proposed method just uses the simulated behaviors for conformance approximation, it is independent of any process model notation.
Table 1. Comparison of approximating the conformance checking using the proposed simulation method and the sampling method.
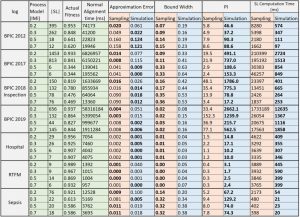
Since we use the edit distance function and do not compute any alignment, even if there is no reference process model and just some of the correct behaviors of the process (e.g., some of the valid variants) are known, the proposed method can approximate the conformance value. The method additionally returns problematic activities, based on their deviation rates.
We implemented the proposed method using both the ProM and RapidProM platforms. Moreover, we applied it to several large real event data and process models. We also compared our approach with the state-of-the-art alignment approximation method. The results show that the proposed simulation method improves the performance of the conformance checking process while providing approximations close to the actual values.
If you are interested in this research, please read the full paper at the following link: https://ieeexplore.ieee.org/document/9230162
If you need more information please contact me via fanisani@pads.rwth-aachen.de
JXES – JSON support for XES Event Logs
This post is by Madhavi Shankara Narayana, Software Engineer in the Process and Data Science team at RWTH Aachen. Contact her via email for further inquiries.
Process mining assumes the existence of an event log where each event refers to a case, an activity, and a point in time. XES is an XML based IEEE approved standard format for event logs supported by most of the process mining tools. JSON (JavaScript Object Notation), a lightweight data-interchange format has gained popularity over the last decade. Hence, we present JXES, the JSON standard for the event logs.
JXES Format
JSON is an open standard lightweight file format commonly used for data interchange. It uses human-readable text to store and transmit data objects.
For defining the JSON standard format, we have taken into account the XES meta-model represented by the basic structure (log, trace and event), Attributes, Nested Attributes, Global Attributes, Event classifiers and Extensions as shown in Figure 1.

The JXES event log structure is as shown in Figure 2.

The plugin for ProM to import and export the JSON file consists of 4 different parser implementations of import as well as export. Plugin implementations are available for Jackson, Jsoninter, GSON and simple JSON parsers.
We hope that the JXES standard defined by this paper will be helpful and serve as a guideline for generating event logs in JSON format. We also hope that the JXES standard defined in this paper will be useful for many tools like Disco, Celonis, PM4Py, etc., to enable support for JSON event logs.
For detailed information on the JXES format, please refer to https://arxiv.org/abs/2009.06363
Columnar and Key-Value Storages in Process Mining
Object-Centric Process Mining: Dealing With Real-Life Processes
This post is by Prof. Wil M.P. van der Aalst, Chairholder of the Process And Data Science group at RWTH Aachen University. Contact him via email for further inquiries.
Techniques to discover process models from event data tend to assume precisely one case identifier per event. Unfortunately, this is often not the case. When we order from Amazon, events may refer to mixtures of orders, items, packages, customers, and products. Payments refer to orders. In one order, there may be many items (e.g., two books and three DVDs). Each of the items needs to handled separately, some may be out of stock, and others need to be moved from one warehouse to another. The same product may be ordered multiple times (in the same order or different orders). Items are combined in packages. A package may refer to multiple items from different orders and items from one order may be scattered over multiple packages. Deliveries may fail due to a variety of reasons. Hence, for one package, there may be multiple deliveries. To summarize: There are one-to-many and many-to-many relations between orders, items, packages, customers, and products. Such one-to-many and many-to-many relations between objects can be found in any process. For example, when hiring staff for multiple positions, there are applications, interviews, positions, etc. In a make-to-order company, many procurement orders may be triggered by a single sales order. Etc.
The scale of the problem becomes clear when looking at an enterprise information system like SAP. One will find many database tables related through keys implementing a one-to-many relationship between different types of business objects. There are also tables to realize many-to-many relations. Although this is common and visible for all, we still expect process models to be about individual cases. A process model may describe the life-cycle of an order or the life-cycle of an item, but typically not both. One can use swim lanes in notations like BPMN, but these are rarely used to denote one-to-many and many-to-many relationships. For sure such approaches fail to capture the above processes in a holistic manner. Object-Centric Process Mining (OCPM), one of PADS key research topics, aims to address this problem.
The usual approach to deal with the problem is to “flatten” the event data picking one of many possible case notions. There may be several candidate case notions leading to different views on the same process. As a result, one event may be related to different cases (convergence) and, for a given case, there may be multiple instances of the same activity within a case (divergence). Object-Centric Process Mining (OCPM) aims to avoid convergence and divergence problems by (1) picking a new logging format and (2) providing new process discovery techniques based on this format. This blog post summarizes part of my presentation given on 19-11-2019 in the weekly PADS Seminar Series (slides are attached).
Object-Centric Event Logs
Input for process mining is an event log. A traditional event log views a process from a particular angle provided by the case notion that is used to correlate events. Each event in such an event log refers to (1) a particular process instance (called case), (2) an activity, and (3) a timestamp. There may be additional event attributes referring to resources, people, costs, etc., but these are optional. With some effort, such data can be extracted from any information system supporting operational processes. Process mining uses these event data to answer a variety of process-related questions.
The assumption that there is just one case notion and that each event refers to precisely one case is problematic in real-life processes. Therefore, we drop the case notion and assume that an event can be related to any number of objects. In such an object-centric event log, we distinguish different order types (e.g., orders, items, packages, customers, and products). Each event has three types of attributes:
• Mandatory attributes like activity and timestamp.
• Per object type, a set of object references (zero or more per object type).
• Additional attributes (e.g., costs, etc.).
This logging format generalizes the traditional XES event logs or CSV files. A traditional event log corresponds to an object-centric event log with just one object type and one object reference per event.
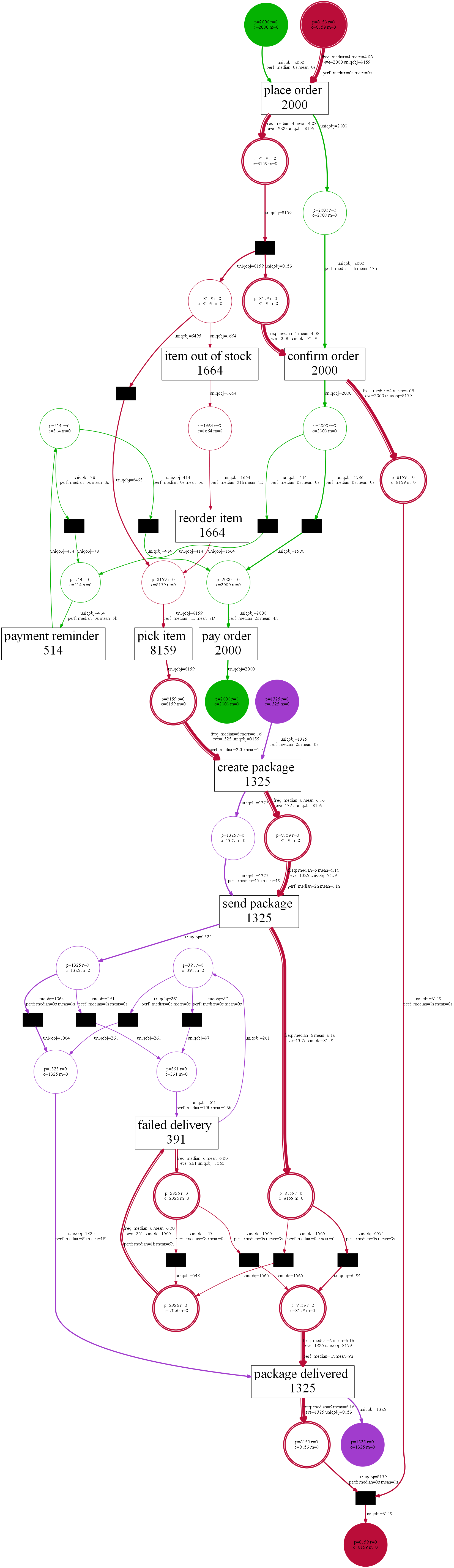
Towards New Discovery Techniques
From an object-centric event log, we want to discover an object-centric process model. For example, Directly Follows Graphs (DFGs) with arcs corresponding to object types and object-centric Petri nets with places corresponding to object types. In the presentation, I described to basic approaches: One for DFGs and one for object-centric Petri nets. See the slides for more information. These baseline algorithms show that object-centric process mining is an interesting and promising research line. Alessandro Berti already implemented various discovery techniques in PM4Py-MDL leading to so-called Multiple Viewpoint Models (MVP models). Anahita Farhang also extended the ideas related to process cubes to object-centric process mining. This provides a basis for comparative process mining in a more realistic setting. An important next step is the evaluation of these ideas and implementations using more complex real-life data sets involving many object types (e.g., from SAP).
Learn More?
1. W.M.P. van der Aalst. Object-Centric Process Mining: Dealing With Divergence and Convergence in Event Data. In P.C. Ölveczky and G. Salaün, editors, Software Engineering and Formal Methods (SEFM 2019), volume 11724 of Lecture Notes in Computer Science, pages 1-23. Springer-Verlag, Berlin, 2019. https://doi.org/10.1007/978-3-030-30446-1_1
2. W.M.P. van der Aalst. A Practitioner’s Guide to Process Mining: Limitations of the Directly-Follows Graph. In International Conference on Enterprise Information Systems (Centris 2019), Procedia Computer Science, Volume 164, pages 321-328, Elsevier, 2019. https://doi.org/10.1016/j.procs.2019.12.189
3. A. Berti and W.M.P. van der Aalst. StarStar Models: Using Events at Database Level for Process Analysis. In P. Ceravolo, M.T. Gomez Lopez, and M. van Keulen, editors, International Symposium on Data-driven Process Discovery and Analysis (SIMPDA 2018), volume 2270 of CEUR Workshop Proceedings, pages 60-64. CEUR-WS.org, 2018. http://ceur-ws.org/Vol-2270/short3.pdf
4. A. Berti and W.M.P. van der Aalst. Discovering Multiple Viewpoint Models from Relational Databases. In P. Ceravolo, M.T. Gomez Lopez, and M. van Keulen, editors, Postproceedings International Symposium on Data-driven Process Discovery and Analysis, Lecture Notes in Business Information Processing. Springer-Verlag, Berlin, 2019. https://arxiv.org/abs/2001.02562
Supporting Automatic System Dynamics Model Generation for Simulation in the Context of Process Mining
This post is by Mahsa Bafrani, Scientific Assistant in the Process and Data Science team at RWTH Aachen. Contact her via email for further inquiries.
Using process mining actionable insights can be extracted from the event data stored in information systems. The analysis of event data may reveal many performance and compliance problems, and generate ideas for performance improvements. This is valuable, however, process mining techniques tend to be backward-looking and provide little support for forward-looking approaches since potential process interventions are not assessed. System dynamics complements process mining since it aims to capture the relationships between different factors at a higher abstraction level, and uses simulation to predict the effects of process improvement actions. In this paper, we propose a new approach to support the design of system dynamics models using vent data. We extract a variety of performance parameters from the current state of the process using historical execution data and provide an interactive platform for modeling the performance metrics as system dynamics models. The generated models are able to answer “what-if” questions.

Figure 1: our proposed framework for using process mining and system dynamics together.
Our proposed framework for using process mining and system dynamics together in order to design valid models to support the scenario-based prediction of business processes shown in Fig. 1. The model creation steps is an important step which we are going to focus on, i.e., the highlighted step.
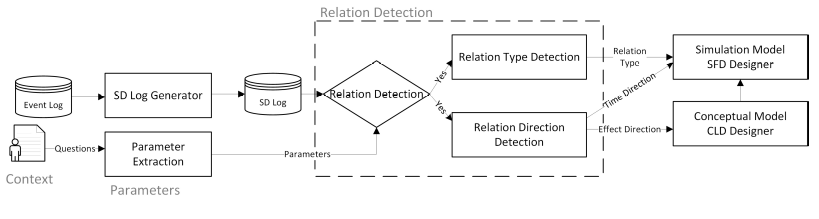
Figure 2: the main approach including the SD-log generation, relation detection, and the discovery of the type and direction of the relations.
Our approach, Fig. 2, continues with the automatic generation of causal-loop diagrams (CLD) and Stock-flow diagrams (SFD). The type of relationship is used to form the underlying equations in SFD and the effect and time directions are automatically used to design the CLD as a backbone of SFD.
In this work, we proposed a novel approach to support designing system dynamics models for simulation in the context of operational processes. Using our approach, the underlying effects and relations at the instance level can be detected and modeled in an aggregated manner. For instance, as we showed in the evaluation, the effects of the amount of workload on the speed of resources are of high importance in modeling the number of people waiting to be served per day. In the second scenario, we focused on assessing the accuracy and precision of our approach in designing a simulation model. As the evaluations show, our approach is capable of discovering hidden relations and automatically generates valid simulation models in which applying the domain knowledge is also possible. By extending the framework, we are looking to find the underlying equations between the parameters. The discovered equations help to obtain accurate simulation results in an automated fashion without user involvement. Moreover, we aim to apply the framework in case studies where we not only have the event data but can also influence the process.
Mahsa Pourbafrani, Sebastiaan J. van Zelst, Wil M. P. van der Aalst:
Supporting Automatic System Dynamics Model Generation for Simulation in the Context of Process Mining. BIS 2020: 249-263
Online Conformance Checking – Incrementally Computing Optimal Prefix-Alignments on Event Streams
This post is by Daniel Schuster, Scientific Assistant in the Fraunhofer FIT. Contact him via email for further inquiries.
The execution of (business) processes generates valuable traces of event data in the information systems employed within companies. Recently, approaches for monitoring the correctness of the execution of running processes have been developed in the area of process mining, i.e., online conformance checking. The advantages of monitoring a process’ conformity during its execution are clear. Deviations are detected as soon as they occur and countermeasures can be initiated immediately to reduce the potential negative effects caused by process deviations.
The figure below outlines the general scenario. During process execution, events are emitted on an event stream. Each event triggers a conformance check, which validates the sequence of activities already executed for a specific process instance against a specific reference process model. Therefore, non-conformity within process executions is detected the moment it occurs.
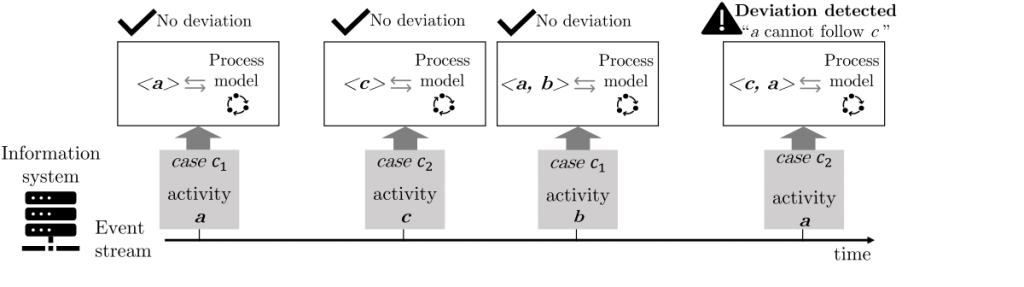
Existing work in online conformance checking so far only allowed for obtaining approximations of non-conformity, e.g., overestimating the actual severity of the deviation. In our paper [1], we present an exact, parameter-free, online conformance checking algorithm that computes conformance checking results on the fly. Our algorithm exploits the fact that the conformance checking problem can be reduced to a shortest path problem, by incrementally expanding the search space and reusing previously computed intermediate results. Thus, as shown by the conducted experiments, we can outperform existing approximation algorithms and at the same time guarantee optimality, i.e., no false negatives in terms of deviation detection.
[1] Schuster, D. and van Zelst, S. J.: Online Process Monitoring Using Incremental State-Space Expansion: An Exact Algorithm. In: 18th Int. Conference on Business Process Management. (2020)
The application of Causal Structural Models in Process Mining
This post is by Mahnaz Qafari, Scientific Assistant in the Process And Data Science group at RWTH Aachen University. Contact her via email for further inquiries.
Processes are highly complicated entities as there are many visible and invisible parameters affecting the journey of each case in a given process. Usually there are a variety of paths taken by different cases and a variety of values assigned to their attributes even for those cases taking the same path. In such a complicated and dynamic environment, it is hard to find those friction points that deteriorate the process in terms of efficiency and other KPIs (Key Performance Indicators), and finding the reasons behind the friction points is even harder. On the other hand, re-engineering a process without this kind of information is hopeless.
The main trend for root cause analysis of an identified problem in a process is applying a machine learning technique on the data gathered from the event log of the process. But these techniques are designed for prediction, not root cause analyses. Blind usage of such results are prone to confusion between causal relationships and correlations. And acting upon them, may results in not only aggravating the current problem but also creating new ones. Having the causes of a problem diagnosed correctly, the next challenging task is anticipating and estimating the effect of changing them on the process.
There are two main frameworks to overcome these hurdles, using random experiment trial and using the theory of causality and its findings. Applying random experiment trials, i.e. randomly setting the values of those attributes that have causal effect on the problem of interest and monitoring their effect on the process, is highly expensive (and sometimes unethical if not impossible) in many situations. The other option is inferring the causal relationships between different attributes of the process using observational data and modeling these relationships by a structural causal model (also called structural equation model). Using this model, it is possible to study the effect of changes imposed by each process factor on the process indicators. Even though finding the causal structure of the process needs the aid of an expert who possess the process knowledge, process mining can benefit a lot from the theory of causality. The general approach for discovering the causal structure of a friction point in a process is depicted in Figure 1.
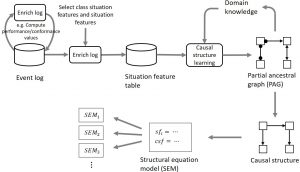
Figure 1: The general approach for structural causal equation discovery.
In our group, we aim to investigate different ways that process mining and causality inference findings can be merged, and result in more advanced and accurate process mining related techniques.
On the importance of privacy metadata for process mining
This post is by Majid Rafiei, Scientific Assistant in the Process And Data Science group at RWTH Aachen University. Contact him via email for further inquiries.
Event logs are the type of data used by process mining algorithms to provide valuable insights regarding the real processes running in a company, organization, hospital, university, etc. However, they often contain sensitive private information that should be analyzed responsibly.
Privacy issues in process mining are recently receiving more attention. Privacy-preserving techniques need to modify the original data, yet, at the same time, they are supposed to preserve the data utility. Different data utility definitions can be used depending on the sensitivity of certain aspects and the goal of the analysis. Privacy-preserving transformations of the data may lead to incorrect or misleading analysis results. Hence, new infrastructures need to be designed for publishing the privacy-aware event data whose aim is to provide metadata regarding the privacy-related transformations on event data without revealing details of privacy techniques or the protected information.
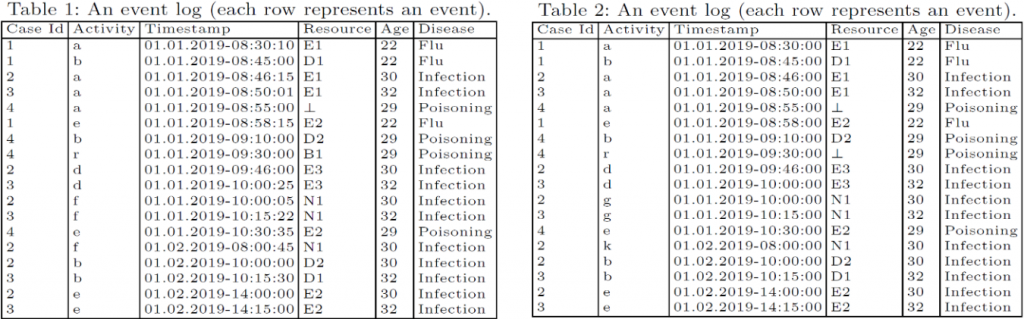
Compare Table 1 with Table 2. They both look like an original event log, right? Can you recognize the relation between these two tables? If one of them was derived from another one, which one is the original? How did the derivation happen? What are the weaknesses of the analyses done on the derived event log?
In fact, Table 2 is derived from Table 1 by randomly substituting some activities (f was substituted with g and k), generalizing the timestamps (the timestamps got generalized to the minutes level), and suppressing some resources (B1 was suppressed). Hence, a performance analysis based on Table 2 may not be as accurate as the original event log, the process model discovered from Table 2 contains some fake activities, and the social network of resources is incomplete.
We have a paper under review to address such challenges by proposing privacy metadata for process mining.
Enhanced Discovery of Uniwired Petri Nets Using eST-Miner
This post is by Lisa Mannel, Scientific Assistant in the Process And Data Science group at RWTH Aachen University. Contact her via email for further inquiries.
More and more processes executed in companies are supported by information systems which record events. Extracting events related to a process results in an event log. Each event in such a log has a name identifying the executed activity (activity name), a case id specifying the respective instance of the process, a time when the event was observed (timestamp), and possibly other data related to the activity and/or process instance. In process discovery, a process model is constructed aiming to reflect the behavior defined by the given event log: the observed events are put into relation to each other, pre-conditions, choices, concurrency, etc. are discovered, and brought together in a process model.
Process discovery is non-trivial for a variety of reasons. The behavior recorded in an event log cannot be assumed to be complete, since behavior allowed by the process specification might simply not have happened yet. Additionally, real-life event logs often contain noise, and finding a balance between filtering this out and at the same time keeping all desired information is often a non-trivial task. Ideally, a discovered model should be able to produce the behavior contained within the event log, not allow for unobserved behavior, represent all dependencies between the events, and at the same time be simple enough to be understood by a human interpreter. It is rarely possible to fulfill all these requirements simultaneously. Based on the capabilities and focus of the used algorithm, the discovered models can vary greatly, and different trade-offs are possible.
Our discovery algorithm eST-Miner [1] aims to combine the capability of finding complex control-flow structures like longterm-dependencies with an inherent ability to handle low-frequent behavior while exploiting the token-game to increase efficiency. Similar to region-based algorithms, the basic idea is to evaluate all possible places to discover a set of fitting ones. Efficiency is significantly increased by skipping uninteresting sections of the search space based on previous results [2]. This may decrease computation time immensely compared to evaluating every single candidate place, while still providing guarantees with regard to fitness and precision. Implicit places are removed in a post-processing step to simplify the model.
In [3] we introduce the subclass of uniwired Petri nets as well as a variant of eST-Miner discovering such nets. In uniwired Petri nets all pairs of transitions are connected by at most one place, i.e. there is no pair of transitions (a1 , a2) such that there is more than one place with an incoming arc from a1 and an outgoing arc to a2. Still being able to model long-term dependencies, these Petri nets provide a well-balanced trade-off between simplicity and expressiveness, and thus introduce a very interesting representational bias to process discovery. Constraining ourselves to uniwired Petri nets allows for a massive decrease in computation time compared to the basic algorithm by utilizing the uniwiredness requirement to skip an astonishingly large part of the search space. Additionally, the number of returned implicit places, and thus the complexity of post-processing, is greatly reduced.
For details we refer the reader to the original papers [1,3]. The basic eST- Miner, as well as the uniwired variant, take an event log and user-definable parameter τ as input. Inspired by language-based regions, the basic strategy of the approach is to begin with a Petri net, whose transitions correspond exactly to the activities used in the given log. From the finite set of unmarked, intermediate places a subset of fitting places is inserted. A place is considered fitting, if at least a fraction of τ traces in the event log is fitting, thus allowing for local noise-filtering. To increase efficiency, the candidate space is organized as a set of trees, where uninteresting subtrees can be cut off during traversal, significantly increasing time and space efficiency.
While the basic algorithm maximizes precision by guaranteeing to traverse and discover all possible fitting places, the uniwired variant chooses the most interesting places out of a selection of fitting candidates wiring the same pair of transitions. Subtrees containing only places that wire the same pair of transitions can be cut off. The output Petri net is no longer unique but highly dependent on the traversal and selection strategy. The approach presented in [3] prioritizes places with few arcs. Between places with the same number of arcs, places with high token-throughput are preferred. This strategy often allows us to discover adequate models, but fails in the presence of long loops which require places with more arcs. To overcome this restriction, we propose to use a reversed strategy, prioritizing places with high token throughput and using the number of arcs as a second criteria. This might slightly decrease the fraction of cut-off candidates but is expected to greatly increase model quality.
The running time of the eST-Miner variants strongly depends on the number of candidate places skippable during the search for fitting places. For the basic approach ([1]) our experiments show that 40-90 % of candidate places are skipped, depending on the log. The uniwired variant ([3]) has proven to find usable models while evaluating less than 1 % of the candidate space in all test cases (Figure 1), thus immensely speeding up the discovery (Figure 2).
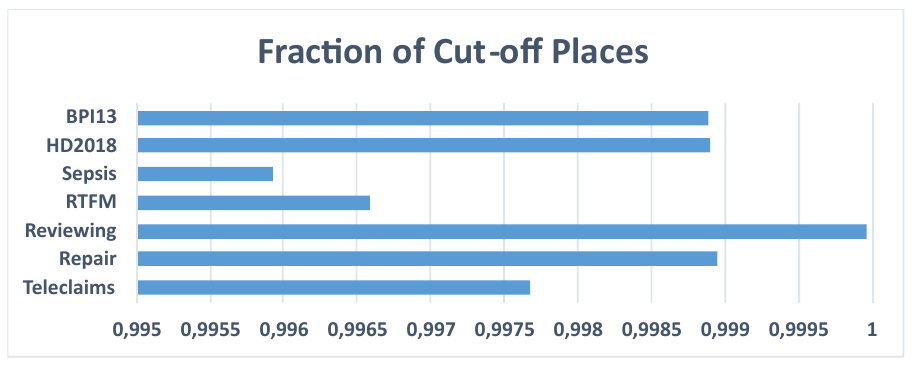
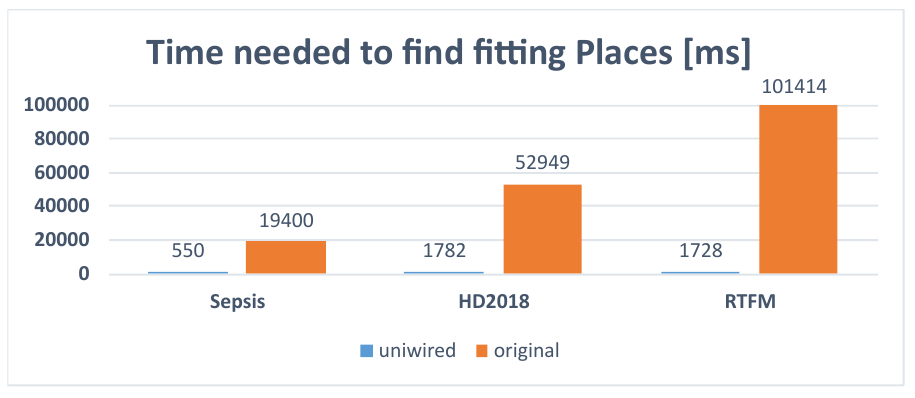
uniwired variant for various logs.
References
[1] Mannel, L., van der Aalst, W.: Finding complex process structures by exploiting the token-game. In: Application and Theory of Petri Nets and Concurrency. Springer Nature Switzerland AG (2019)
[2] van der Aalst, W.: Discovering the ”glue” connecting activities – exploiting monotonicity to learn places faster. In: It’s All About Coordination – Essays to Celebrate the Lifelong Scientific Achievements of Farhad Arbab (2018)
[3] Mannel, L., van der Aalst, W.: Finding uniwired Petri nets using eST-miner. In: Business Process Intelligence Workshop 2019. Springer (to appear)

